We published a paper on skimmer performance in the January 2009 issue of Advanced Aquarist magazine that detailed, for the first time, an experimental methodology to provide meaningful metrics for both the rate at which skimmers removed organics and the extent of the removal of these organics from aquarium water (Feldman, 2009). Highlights of these earlier studies included:
- Development of a mathematical representation of the skimming process based upon a “continuously stirred reactor” model for both the skimmer and the reservoir (tank) with a given water flow rate between them.
- Application of that mathematical formalism to both (a) a model system featuring removal of Bovine Serum Albumin (BSA) as a test case protein in freshly prepared saltwater, and (b) authentic TOC (Total Organic Carbon) removal in reef tank water. Key experimental parameters extracted from this mathematical modeling included the rate constant, k, for organic (BSA or TOC) removal, which is a singular metric reflecting the intrinsic capacity of a given skimmer to remove the organics in question, and the total % of the available organics (BSA or TOC) that were removed before the skimmer “flatlined””.
- Analysis of these data for four representative skimmers; a EuroReef CS80 needlewheel skimmer, a Precision Marine ES100 venturi skimmer, a Precision Marine AP624 airstone skimmer, and an ETSS Evolution 500 downdraft skimmer.
- Conclusions about relative skimmer performance based upon these measurements:
- All four skimmers removed both BSA and TOC with similar rate constants; in short, “bubbles is bubbles”, and there was no significant difference between these four skimmers in their intrinsic abilities to strip organics from saltwater.
- Only about 20 – 30% of the measurable TOC in reef tank water was removed by skimming, whereas almost all of the BSA was removed from saltwater by skimming.
Over the intervening year, we have continued and expanded these studies of skimmer performance in several directions. In this article, we report the results of these efforts. Specifically, we have:
- Modified our mathematical model to take into account the observation that there is a (significant) component of TOC that is not skimmable. We have applied this new model to the old skimmer data as well as to new data with new skimmers.
- Examined the performance of three new skimmers, all of which have bubble plates; the Bubble King Mini 160 needlewheel skimmer, the Royal Exclusiv 170 Cone needlewheel skimmer, and the Reef Octopus 150 recirculating pinwheel skimmer.
The Modified Mathematical Model
The mathematical model derived in the January 2009 Advanced Aquarist article was based upon four assumptions:
- The water reservoir can be treated as a continuously stirred reactor.
- The skimmer mixing volume can be treated as a continuously stirred reactor.
- The reservoir volume is much larger than the skimmer mixing volume.
- The rate of TOC removal in the skimmer is proportion to the amount of TOC present in the water.
There is no reason to doubt the validity of assumptions 1 – 3. However, assumption #4 does not take into account the experimental observation that only some of the TOC in reef tank water is susceptible to removal by skimming. Thus, a more appropriate and general starting point would involve explicitly breaking down TOC into two functionally distinct components:
- [TOCl], or labile TOC that the skimmer will remove
- [TOCr], or refractory TOC that the skimmer won’t remove
With this distinction made, the prior math can be adapted to arrive at a slightly modified expression that once again allows extraction of the two quantities of interest from the raw data: the mass transfer rate constant, k (units = per minute), for TOCl removal, and the total amount of TOC remaining, TOCr, when the skimmer is not pulling out any more (labile) organics from the reservoir water. The recirculating reservoir/skimmer system (Fig. 1) maps quite closely onto a fundamental textbook problem in mass transfer/fluid flow encountered in introductory chemical engineering courses called the “continuously stirred” or “well-stirred” reactor problem. (Felder, 2005) In this instance, both the skimmer and also the reservoir can be treated as “well-stirred reactors” with a given flow Q between them. A component of the water is depleted in the skimmer by bubble-mediated removal.
Where:
- [TOCT]r = the total concentration of TOC in the reservoir, in ppm. Note that:
- [TOCT]r = [TOCl]r + [TOCr]r, where [TOCl]r = labile TOC that the skimmer will remove, and [TOCr]r = refractory TOC, which the skimmer will not remove
- [TOCT]s = the total concentration of TOC in the skimmer, in ppm. Note that:
- [TOCT]s = [TOCl]s + [TOCr]s, where [TOCl]s = labile TOC that the skimmer will remove, and [TOCr]s = refractory TOC, which the skimmer will not remove
- Q = the volumetric water flow rate, in gal/min
- Vr = the volume of the reservoir, in gal (30 gal)
- Vs = the mixing volume of the skimmer, in gal
It is important to note that not all of the TOC present in reef tank water is susceptible to skimmer-mediated removal – some types of TOC are not picked up by bubbles. To account for this observation, we have divided the TOC into a labile, or skimmer-removable component [TOCl], and a refractory, or skimmer-inert component [TOCr]. Therefore, the total TOC that we measure experimentally is the sum of these two types of TOC: [TOCT] = [TOCl] + [TOCr]. However, only the labile TOC’s concentration [TOCl] is changing upon skimmer action; the refractory TOC’s concentration, [TOCr] does not vary. Thus, we can confine our mathematical derivation to this labile TOC, TOCl, and at the end take into account the fact that experimentally, we can only measure the total TOC, TOCT.
Since both “reactors” are interconnected, the level of the labile TOC component will drop in the reservoir as well, and our task will be to develop a mathematical model that relates the removal in the skimmer with the measured depletion in the reservoir. In our experimental setup, a liquid volume Vr (reef tank water in a Rubbermaid tub) has an input stream and an output stream, and TOC in the water becomes depleted over time via bubble-mediated removal in a skimmer with mixing water volume Vs (see Fig. 1). Inspection of the skimmers in action permits measurement of this “active” skimmer mixing volume, which is the value that we will use for Vs. For the purposes of this analysis, we will assume that all of the active volume is water; that is, we will ignore the void volume of the bubbles, as we cannot independently assess the relative contributions of bubbles and water. This assumption will introduce an error into the calculations, but that error
should be systematic for all skimmers, and since we are interested in relative and not absolute skimmer performance, this error should not affect the conclusions. Knowledge of the precise mechanism by which the skimmer’s bubbles removes the water component(s) is not required; all that we need to know is that the concentration of the measured water component (TOCT in this case) is diminishing with time in the reservoir.
It is essential for solving this problem that both the reservoir and the skimmer water volumes are well mixed to avoid concentration gradients. The reservoir water mixing in the experiments described below is provided by the skimmer return flow and by two powerheads in the reservoir. We independently tested the “well mixed” assumption in the reservoir by sampling TOC levels at a given time point at different locations (i.e., top, bottom, left side, right side) during a skimmer run. We observed that the site-to-site variation in TOC levels at different locations was no greater than the sample-to-sample variation at one location (both ~ 10%), suggesting that there is no reason to suspect that the “well mixed” assumption is not applicable. The mixing in the skimmer reaction chamber is provided by both rapid water movement and the agitation caused by the motion of the bubble stream. We have no independent experimental measurement/confirmation of mixing behavior in the skimmer.
The application of this mathematical approach to the protein skimmer problem leads ultimately to two important equations, labeled 22 and 24 below. The complete mathematical derivation (i.e., Eqs. (1) – (21)) can be found in the next section. This derivation that is largely taken from the 2009 Advanced Aquarist article. This new version of the derivation takes into account the presence of refractory TOC, TOCr.
(22) [TOCT]r = ([TOCT]o – [TOCr]o)•e-[k•Q/(Vr•(k + Q/Vs))]•t + [TOCr]r
Eq. (22) provides the means to extract the desired quantity, the rate constant k, from the experimental data. Experimentally, the quantities [TOCT], [TOCT]o, time t, Q, Vs, and Vr can all be measured. In addition to this expression which determines the amount of TOC present at a given time t, we can also manipulate the mathematical formula to arrive at an equation that defines the rate of TOC removal, a metric that takes into account the rate constant k as well as the flow Q, and the skimmer and reservoir volumes, Vs and Vr, respectively.
(24) rate = d[TOCl]r/dt = -[Q/(Vr•(1 + Q/k•Vs))]• [TOCl]r
This version of the rate expression has the useful property of revealing that when Q/k•Vs >>1,
(25) rate = -(Vs•k/Vr)• [TOCl]r
That is, under the conditions where Q/k•Vs >> 1, the rate only depends on the rate constant k, the skimmer volume Vs, and the tank volume Vr; it does not depend upon the flow rate Q.
Conversely, if Q//k•Vs << 1, then the rate expression reduces to
(26) rate = – (Q/Vr)• [TOCl]r
That is, the rate only depends on the flow rate Q and the tank volume; it does not depend upon either the skimmer size of the rate constant for TOC removal.
For the Royal Exclusiv 170 cone, the Bubble King mini 160, the ETSS evolution 500 and the Reef Octopus 150, Q/k•Vs > 5 (see below), so invoking the simplification of Eq. (25) will introduce less than a 20% error. For the Precision Marine ES100, the Precision Marine AP624 airstone, and the EuroReef CS80, Q/k•Vs is between 1 and 5, and the simplification of Eq. (25) cannot be used. In no case is Q/k•Vs << 1.
Finally, we can easily calculate the amount (%) of TOC removed in a given experiment by simply subtracting [TOCr]r, a value available from Eq. (22), from the beginning TOC concentration, [TOTT]0, and dividing by [TOCT]0.
(27) % of TOC removed = 100 x ([TOCT]0 – [TOCr]r)/[TOCT]0
The Math Behind It
(skip ahead to the next heading if you wish to skip the math behind the modeling)
The fundamental physical property of the system that we will rely on to develop a mathematical model for skimmer performance is called mass balance; conservation of mass dictates that mass (matter, in this case TOC) cannot be created or destroyed, and so the amount of TOC depleted from the reservoir must be equal to the amount of TOC that is removed by the skimmer’s bubbles. The fundamental mass balance equation is given in Eq. (1). Details can be found in the Wikipedia entry for “Mass Balance” and “Continuously Stirred-Tank Reactor“.
(1) input + generation = output + accumulation
For the problem at hand, there is no generation of TOC; rather, TOC is removed by the skimmer’s bubbles, so we will replace the “generation” term with “removal” (actually, just the negative of generation). In addition, since there is no TOC generation, there will be no TOC accumulation; rather, TOC is depleted in the system over time, so we will replace the “accumulation” term with “depletion” (just the negative of accumulation). So, the new mass balance expression applicable to both the reservoir, and independently, the skimmer is:
(2) input + removal = output + depletion
We will focus on the labile TOC in the reservoir first. There is no explicit TOC removal in the reservoir, so “removal” in Eq. (2) = 0. The input is equivalent to the mass of TOC added over time, say milligrams-per-minute (mg/min). In fact, since one term of Eq. (2) has units of mg/min (or more generally, mass/time), then all of the terms in this equation must be expressed in these units. The mass (amount) of TOC added in the input stream is the concentration of TOC, [TOCl]s (in mg/gal) times the volumetric flow rate of the input stream, Q (Q in gal/min). That is,
(3) mass of TOC added over time in input stream = Q•[TOCl]s
Note how the units of these terms are consistent: Q (in gal/min) • [TOCl]s (in mg/gal) = mg/min units, which is just what the “mass of TOC added over time” requires. The output stream of the reservoir can be treated in a similar manner:
(4) mass of TOC removed over time in output stream = Q•[TOCl]r
So, referring back to Eq. (2), with removal = 0, we have
(5) Q•[TOCl]s = Q•[TOCl]r + depletion
What mathematical expression can we use for “depletion”? The amount of TOC in the reservoir volume Vr is simply the product of the TOC concentration, [TOCl]r, and the volume:
(6) amount of TOC in the reservoir = Vr•[TOCl]r
We can simply define “depletion” to mean the rate of change (decrease) in the TOC amount in the reservoir over time. Note that once again, the units of this term are in mass/time (“mg/min”).
(7) depletion = Vr•d[TOCl]r/dt
Now, returning to Eq. (5), we can insert the depletion term and generate the full mass balance expression for the reservoir:
(8) Vr•d[TOCl]r/dt = Q•([TOCl]s – [TOCl]r), where:
- Vr = the total volume of the reservoir water, in gal
- [TOCl]r = the concentration of labile TOC in the reservoir at any time t and also the concentration of labile TOC in the stream leaving the reservoir and entering the skimmer
- Q = the volumetric flow through the system, in gpm
- [TOCl]s = the concentration of labile TOC in the stream leaving the skimmer and entering the reservoir
Eq. (8) says that the change in the amount of TOC in the reservoir (the left hand side) is equal to the difference between the reservoir input and output TOC concentrations ([TOCl]s – [TOCl]r) times the flow rate (the right hand side). Note that this expression includes information about TOC concentrations in both the reservoir and the skimmer.
A similar expression can be developed for the fate of the TOC concentration just in the skimmer. However, in this case, “removal” does not equal 0, as the bubbles in the skimmer actively remove the organic impurity. So, from Eq. (2),
(9) Vs•d[TOCl]s/dt = Q•([TOCl]r – [TOCl]s) + removal
We must include another term (removal) in Eq. (9) that explicitly accounts for this TOC removal in order to maintain the required mass balance. This TOC removal term must take into account the function of the bubbles. The fundamental chemical equation for TOC removal by the bubbles is:
(10) TOC + bubbles → TOC•bubbles
This simple equation undergirds the assumption that allows the mathematical analysis to proceed: the key assumption is that the rate of labile TOC removed by the skimmer’s bubbles is proportional to the amount of labile TOC present in solution. This assumption permits us to connect the [TOC] changes that happen in the skimmer with the [TOC] changes that happen in the reservoir. Since the bubbles are continually being introduced in large excess compared to the TOC concentration in solution, the “concentration” of the bubbles remains for all intents and purposes constant, and so we do not have to worry about how changes in bubble concentration might influence the rate of TOC removal. This model (and its underlying assumptions) greatly simplifies the mathematical analysis. In terms of the discipline of chemical kinetics, this approach is called the “pseudo-first order” approximation. So, the amount of labile TOC in the active skimmer reaction chamber volume Vs is given by the concentration times the volume:
(11) amount of labile TOC in the active water volume of the skimmer = Vs•[TOCl]s
By the assumption discussed above, the rate of labile TOC removal by the bubbles is proportional to the amount of labile TOC present:
(12) rate of labile TOC removal by the bubbles µ -Vs•[TOCl] s
Note that we must include a “-” sign in front of Vs•[TOCl]s because the amount is decreasing with time. We can introduce a proportionality constant, k, to convert Eq. (12) into an equality.
(13) rate of TOC removal by the bubbles = – k•Vs•[TOCl]s
The term k•Vs•[TOCl]s must have units of mass/time (i.e., mg/min) in order to “fit” into Eq. (9). Since Vs•[TOCl]s has units of mass (mg), then k must have units of /time (i.e., per min). As such, k is often referred to as a rate constant; it expresses how something changes over time (“per min”). This proportionality constant is not just a mathematical convenience. It will report on a fundamentally important property of a skimmer. The constant k can be viewed as a measure of how efficiently the skimmer/bubbles remove TOC. The efficiency of TOC removal is a complex function of many factors (skimmer geometry, bubble size/density, bubble residence time, solution diffusion, mass transfer to the bubble, foam coalescence, binding to the bubble surface, etc.). In fact, it is just this value k that we are after; k is actually a singular measure of skimmer efficiency in removing TOC. The larger that k is, the faster that a given skimmer will remove TOC. Thus, k is an intrinsic measure for TOC removal, and it reflects, in the aggregate, all of the parameters that contribute to the efficiency of TOC removal for a given skimmer. However, k does not offer any insight into which parameters, in particular, are more or less important in determining skimmer performance. We can measure experimentally k for different skimmers, and compare these values. Skimmers with larger k values will be more efficient (i.e., faster) at removing TOC from aquarium water. So, by including the information in Eq. (13) in Eq. (9), we have:
(14) Vs•d[TOCl]s/dt = Q•([TOCl]r – [TOCl]s) Vs•k•[TOCl]s
This rather complex equation is important because, for the first time, we have mathematically linked the experimentally (indirectly) measurable quantity, the concentration of labile TOCl in the reservoir, [TOCl]r (measured via [TOCT]r – [TOCr]r), with quantities specific to the skimmer (Vs, [TOCl]s). However, Eq. (14) as written is difficult to manipulate, so we will define a new mathematical quantity that will help us simplify the math and arrive at a very useful expression. We define a dimensionless time t = Q•t/Vr. Applying this definition to Eq. (14), we can generate the following expression:
(15) (Vs/Vr)•d[TOCl]s/dt = [TOCl]r – [TOCl]s – Vs•k•[TOCl]s/Q
The purpose for this seemingly arbitrary definition/substitution exercise now can be revealed. The use of t allows us to isolate the dimensionless quantity Vs/Vr, which is the ratio of the active skimmer volume to the reservoir volume. We can inject a dose of physical reality into the mathematics at this point. The reservoir volume (30 gallons) is much larger than the skimmers’ volumes (0.62 – 1.3 gallons, see below) and so the ratio Vs/Vr hovers in the 0.02 – 0.04 range. If the second term in the left-hand part of Eq. (15), d[TOCl]s/dt, is not too large, then the Vs/Vr term will dominate, and we can neglect the entire left-hand term of Eq. (15); that is, we can, to a first approximation, set (Vs/Vr)•d[TOCl]s/dt = 0. We have obtained experimental justification for the claim that d[TOCl]s/dt is not large.
By applying this approximation, we can relate the labile TOC concentration in the skimmer, [TOCl]s, to the TOC concentration in the reservoir, [TOCl]r:
(16) 0 = [TOCl]t – [TOCl]s – k•[TOCl]s•Vs/Q, or
(17) [TOCl]s = [TOCl]r/(1 + k•Vs/Q)
We now can plug this [TOCl]s value back into Eq. (8) and divide both sides by Vr:
(18) d[TOCl]r/dt = (Q/Vr)•([TOCl]r/(1 + k•Vs/Q) – [TOCl]r)
Rearranging the various terms yields a differential equation:
(19) d[TOCl]r/[TOCl] r = -[k•Q/(Vr•(k + Q/Vs))]•dt,
and solving the differential equation yields
(20) Ln([TOCl]r/[TOCl] 0) = -[k•Q/(Vr•(k + Q/Vs))]•t
If we could measure just the labile component of TOC, [TOCl]r, then Eq. (20) would suffice for our goals; we would then experimentally measure [TOCl]r at different times t, and upon graphing -Ln([TOCl]r/[TOCl] 0) vs. t, we would be able to extract out the desired quantity, k. However, we cannot measure just the labile component of TOC; we can only measure the total TOC, [TOCT]r, and the refractory TOC, [TOCr]r. Thus, we have to substitute [TOCl] = [TOCT] – [TOCr] into Eq. (20).
(21) Ln{([TOCT]r – [TOCr]r)/([TOCT)o – [TOCr]o)} = -[k•Q/(Vr•(k + Q/Vs))]•t
This expression can be rearranged for convenience into the form:
(22) [TOCT]r = ([TOCT]o – [TOCr]o)•e-[k•Q/(Vr•(k + Q/Vs))]•t + [TOCr]r
Eq. (22) provides the means to extract the desired quantity, the rate constant k, from the experimental data. Experimentally, the quantities [TOCT], [TOCT]o, time t, Q, Vs, and Vr can all be measured. Plotting the experimentally measured [TOCT] vs. time t will give an exponential decay-type curve, and that curve can be fit to the general equation
(23) Y = A•e-Bx + C
where:
- A = [TOCT]o – [TOCr]o
- B = k•Q/(Vr•(k + Q/Vs)), and
- C = [TOCr]r
Note that [TOCT]0 is the concentration of TOC at t = 0, the beginning of the experiment. Remember that the rate constant k for TOC removal has the units min-1; that is, k is expressed as “per minute”. Finally, [TOCr]r can be found from this graphing procedure, and then [TOCl]r can be calculated via [TOCT]r – [TOCr]r.
Equation (18) expresses a subtle but important aspect of this modeling; the difference between a rate and a rate constant. Our interest in comparing different skimmers focuses our attention on the rate constant k. As discussed above, this single value is an aggregate measure of the efficiency of a given skimmer in removing TOC; it reflects all of the intimate structural and molecular details that impact on organics removal (see above). However, the overall rate of TOC removal (different than the rate constant!) is expressed by Eq. (18) and rewritten in a more convenient form below as Eq. 24. That is, the rate is defined as the depletion of TOC over time, or d[TOCl]/dt (the left hand part of Eq. (18)). Eq. (18) indicates that the rate of TOCl removal is a complex function of k, the flow rate Q, and the system volumes Vs and Vr. Thus, increasing k, or increasing Q, or decreasing Vr will all increase the overall rate of TOCl removal. There is nothing in the mathematical derivation to indicate whether k itself is a function of Q or not. This point was tested through experiment with the Reef Octopus 150 skimmer, and there was very little change in k as the flow rate increased from 162 gph up to 390 gph (see below).
It is possible to algebraically manipulate the complex “k” term of Eq. (18) to arrive at the following form:
(24) rate = d[TOCl]r/dt = -[Q/(Vr•(1 + Q/k•Vs))]• [TOCl]r
The Experimental Design
We examined how TOC levels varied over time in reef aquaria prior to initiating the skimmer studies. These preliminary experiments measuring TOC levels in reef aquaria were conducted by removing 20 – 30 mL water samples at the indicated times using VWR brand TraceClean vials equipped with Teflon septa. The vials were dipped upside down under the tank water surface a few inches and then inverted to fill. The vial contents were frozen immediately by placing them in a – 23oC freezer, and at a later date quickly thawed by placing them in a warm water bath prior to analysis using a Shimadzu 5000 TOC Analyzer calibrated with potassium phthalate as per instrument specifications. Blank samples (Shimadzu pure water – guaranteed < 0.1 ppm of C) were run periodically throughout an experimental run, and blank subtraction preceded final data analysis.
The actual skimmer trials were run as described in the earlier Advanced Aquarist article. All skimmers were cleaned prior to their initial use by running distilled water through them for 24 hr (3 times) and then freshly prepared saltwater for 24 hr (2 times). In the actual experiments, 30 gallons of reef tank water was removed 45 – 60 min after feeding the tank with Reef Nutrition products (Rotifeast, Phytofeast, Oysterfeast, and arctipods), some meaty food (mysis shrimp, chunks of shrimp/clams), and some flake food. The tank’s skimmer and granular activated carbon (GAC) filter were off during this feeding period. At the water removal time, no visible evidence of food or food residue remained. The 30 gallons of tank water were transferred to a Rubbermaid tub equipped with two Maxijet 1200 powerheads for circulation and a heater set at 77 oF. The skimmer, which was thoroughly cleaned between each run, was placed at the appropriate height in (or above) the water (manufacturer’s recommendation) and the pump (again, manufacturer supplied or recommended) was turned on. Any output valve adjustments were quickly made to ensure that the water/foam level was within the manufacturer’s recommendations. Approximately 20 – 30 mL water samples were removed at T = 0, 10, 20, 30, 40, 50 60, 90, and 120 min; each water sample was placed in a VWR brand TraceClean vial with a Teflon septum in the cap. The water samples were removed by dunking the vial upside down with tongs about 6″ below the water surface, inverted to fill, and then immediately placed in a -23oC freezer pending analysis. The water samples were all thawed quickly and the TOC concentrations were measured using the Shimadzu 5000 TOC analyzer as described above.
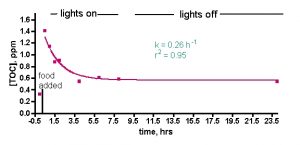
Figure 2a. TOC levels vs. time after tank feeding, no skimmer or GAC. (a) Raw data from a typical run.
Results
We ran two experiments designed to probe the question, “Is a skimmer really necessary to keep TOC levels low in a reef tank?” prior to examining specific skimmers. The answer to this question is obviously “Yes!” according to skimmer manufacturers, but there are alternative aquarium husbandry techniques (i.e., algae filtration) whose practitioners do claim success, thus raising the larger question of skimmer necessity. Of course, tank water skimming has other substantial benefits in terms of oxygenation and gas exchange in general, but the claim of TOC removal is one that we wished to test.
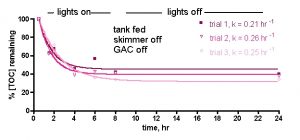
Figure 2b. TOC levels vs. time after tank feeding, no skimmer or GAC. (b) Aggregate runs, with [TOC] expressed as % remaining to normalize the individual trials.

Figure 3. Normalized TOC levels vs. time after feeding for a skimmer (no GAC) reef tank. Skimmer = H&S 200-1260.
Now, if we were to repeat the above experiment, but this time employ an H&S 200-1260 recirculating needlewheel skimmer running throughout the 24-hr experimental period, what might we expect? If the skimmer also aggressively contributes to the removal of TOC from the tank water, we might anticipate that the drop-off in TOC level over time might be precipitous, or at least more rapid than that observed during the skimmerless experiments. This type of increase in rate of TOC removal would be expressed in the k term; a larger k value would signify a faster removal of TOC from the reef tank water. The results, again in triplicate, are illustrated in Fig. 3.
It is apparent that the similarity in k values for the skimmed and the unskimmed tank trials do not support the notion that the skimmer is contributing in any material way to the removal of TOC from the reef tank water. That is, the natural TOC consumers (bacteria and other organisms) are completely adequate for returning the post-feeding TOC levels to approximately baseline values after ~ 24 hrs – the skimmer isn’t required in this process. These observations therefore do not support the conventional wisdom that a skimmer is obligate for lowering and/or maintaining low TOC levels in a reef tank.

Figure 4. Cumulative TOC readings on a 500-gallon reef tank over 30 days; two different skimmers tested over two successive months. Left: DIY downdraft skimmer. Right: DIY needlewheel skimmer.
However, these data may not tell the whole story. If the issue is gradual accumulation of TOC over time, then perhaps a 24-hr experimental period is not sufficient to detect this type of a possible long-term trend. So, we ran a second experiment that was designed to probe for gradual accumulation of TOC over a 30-day time period. Is this instance, two separate trials were pursued, each with a different skimmer, which itself along with GAC was running continuously during the 30-day period. What might we expect? If naturally occurring TOC consumers like bacteria clear up most, but not quite all of the TOC introduced by feeding (its impossible to tell over the 24-hr time period of the above experiments), then perhaps there will be some “remainder” that either accumulates over time, or with skimming, perhaps is removed by that method. These experiments were not run on the author’s reef tank like the remainder of the experiments described in this article; rather, they were run on Sanjay Joshi’s 500-gallon reef tank. The two skimmers tested in these trials were both homemade; one is a modified ETSS-style downdraft with a Beckett head, and the other is a much more elaborate copy of a Bubble King skimmer complete with Red Dragon pump, bubble plate, etc (see Fig. 4). The experiment began in each case after a large water change, and the water was not changed, nor were there any significant changes in livestock, during the month-long trials. The skimmer was run continuously with weekly cleaning, and GAC was run continuously for the month without recharging. Water samples were removed as previously described and stored frozen pending TOC analysis. The water samples were removed 12 hours after feeding each day. The data are presented in Fig. 4.
Two meaningful conclusions can be drawn upon examination of these data. First and foremost, the TOC level does increase over time. Thus, neither microbial action nor skimming removes all of the accumulating TOC. Second, the less presumptuous downdraft skimmer appears to do a better job at holding TOC levels lower over the course of a month compared to the Bubble King clone. In more quantitative terms, the aggregate TOC values averaged for both skimmers increase from about 0.53 ppm of C at T = 0 to about 0.95 ppm of C at T = 30 days; a 79% increase! If Sanjay would have performed water changes of just 10% at 7, 14, 21, and 28 days during this experimental time course, the TOC level would have increased to only 0.66 ppm of C – a 25% increase. Thus, this experiment illustrates the importance of conducting regular water changes as a means to keep organic nutrients in check.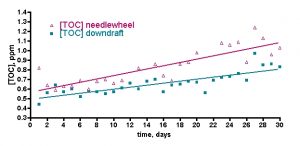
Skimmer Comparison Studies
Our original studies described in the January 2009 Advanced Aquarist article featured exploration of two experimental systems; BSA in freshly prepared saltwater and TOC in authentic reef tank water. Subsequent to these studies, we embarked on a project designed to provide elemental and in many cases chemical information about the constituents of crude skimmate, as discussed in a companion article to be published in Advanced Aquarist. One unassailable conclusion from those studies was that skimmate contains little, if any, protein, and so the use of a protein (BSA) to measure skimmer performance no longer seemed like a relevant model system. Consequently, the performance tests run on the new trio of skimmers introduced below used only TOC removal from authentic reef tank water as the significant metric; the BSA studies were dropped. Three figures-of-merit were extracted from the mathematical analysis described earlier:
- the rate constant, k, for TOC removal
- a quantity (k•Q/(Vr(k + Q/Vs)) proportional to the overall rate, d[TOC]/dt, for TOC removal, and
- the % of the initial TOC that the skimmer removed
The rate constant k was derived from plotting Eq. (22) with experimental data for [TOCT]0, Q, Vr and Vs. The % TOC removed was found through Eq. (27), and the quantity (k•Q/(Vr(k + Q/Vs)), which is proportional to the rate of TOC removal, is derived from Eq. (22) – it is the exponent found through curve fitting. Note that this number is a function of several experimental quantities, including the rate constant k; some simplification is possible under the conditions specified with the discussion of Eq. (25). Pictures of the seven skimmers examined in this and the earlier study are provided in Fig. 5. The reservoir volume, Vr, was always 30 gallons.

Figure 5a. Pictures of the skimmers tested in this and the earlier study, with measured mixing volumes.
Examples of raw data collected in these experiments are illustrated in Fig. 6 for two representative skimmers, the EuroReef CS80 and the Bubble King mini 160. These data sets describe how the measured TOC values in the 30 gallon reservoir drop over the 2-hr time period of the experiment. The squares and triangles are the actual physical measurements; the lines are the mathematical curve fit from Eq. (22). For both of the skimmer runs depicted, r2 > 0.9, which indicates that the match between data and model is quite good. It is essential to demonstrate through a control experiment that the depletion in TOC is actually due to the skimmer’s action and not, for example, due to either absorption onto the plastic of the reservoir/pump/skimmer or consumption by water borne bacteria (→ CO2, lost upon analysis). The black line of Fig. 6 is just this control; the reservoir was filled with tank water, but the skimmer was not run. Samples were removed periodically over 2 hours and assayed for TOC content. The data show that at least over the time course of the experiment, the TOC level remains constant – there is no loss that can be attributable to non-skimmer actions. Visual inspection of the EuroReef and Bubble King data draws out some obvious conclusions; the EuroReef seems to drop the TOC level a little faster than the Bubble King, but the Bubble King seems to drop the TOC level to a lower value than the EuroReef at the 2-hr mark. Whereas these observations can provide a qualitative sense of one skimmer’s performance vs. another skimmer, a far more valuable outcome of these experiments would be to quantify these differences, and that is where the mathematical modeling/analysis discussed earlier comes in. As detailed with the discussion of Eq. (22), numerical values of both the rate of TOC depletion and the amount of TOC in total removed can be extracted from these data sets.
A tabular survey of the experimentally derived values for the three metrics detailed above is given in Table 1. We have recalculated these quantities with the new mathematical model for the four skimmers reported in the January 2009 Advanced Aquarist article based upon the original raw data, and these new values are reported in Table 1 as well. As an aside, the flow rates for all but the Bubble King and Royal Exclusiv skimmers were measured by simply timing the filling of a vessel of predetermined volume. The two remaining skimmers had flow exit ports below the level of the reservoir water, and so a direct measurement as above could not be performed. A workaround was developed by constructing the plumbing adaptation illustrated in Fig. 5b; the output pipe plumbing was brought exactly to the reservoir water level, thus minimizing any issues with head pressure loss. We then timed the filling of the blue vessel to a predetermined volume. Note that the Red Dragon Bubble King 1000 pump in the Royal Exclusiv 170 cone pushes water about twice as fast through the skimmer body as does the smaller Red Dragon mini Bubble King 600 pump in the Bubble King mini 160.
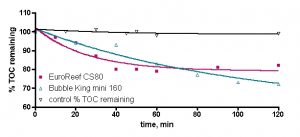
Figure. 6. Representative raw experimental data for the EuroReef CS80 and Bubble King mini 160 skimmers.
| Skimmer | Flow Q, g/min | k, min-1 | r2 for the data set | ave k, min-1 | (k•Q/(Vr(k+Q/Vs))µ rate, min-1 | ave ∝ rate, min-1 | % drop in TOC | ave % drop in TOC |
|---|---|---|---|---|---|---|---|---|
| EuroReef CS80 needlewheel | 2.80 | 0.67 | 0.88 | 2.2 ± 1.5 | 0.012 | 0.032 ± 0.01 | 17 | 20 ± 6 |
| 2.96 | 0.79 | 0.89 | 0.014 | 32 | ||||
| 2.90 | 4.61 | 0.96 | 0.048 | 17 | ||||
| 2.90 | 3.30 | 0.80 | 0.040 | 16 | ||||
| 2.87 | 1.82 | 0.90 | 0.027 | 26 | ||||
| Precision Marine ES100 venturi | 3.59 | 3.22 | 0.50 | 2.3 ± 0.8 | 0.060 | 0.048 ± 0.01 | 17 | 24 ± 4 |
| 3.74 | 2.31 | 0.89 | 0.051 | 27 | ||||
| 3.58 | 1.27 | 0.65 | 0.034 | 24 | ||||
| Precision Marine AP624 airstone | 3.41 | 0.48 | 0.89 | 0.84 ± 0.4 | 0.017 | 0.027 ± 0.008 | 26 | 31 ± 4 |
| 3.49 | 0.72 | 0.94 | 0.024 | 35 | ||||
| 3.60 | 1.43 | 0.87 | 0.040 | 32 | ||||
| 3.55 | 0.75 | 0.86 | 0.025 | 32 | ||||
| ETSS Evolution 500 downdraft | 6.63 | 0.97 | 0.87 | 1.3 ± 0.5 | 0.025 | 0.031 ± 0.008 | 41 | 30 ± 12 |
| 5.83 | 1.90 | 0.92 | 0.043 | 31 | ||||
| 6.12 | 0.98 | 0.85 | 0.025 | 18 | ||||
| Reef Octopus 500 recirc pinwheel | 2.69 | 0.19 | 0.95 | 0.17 ± 0.03 | 0.0076 | 0.0071 ± 0.001 | 39 | 35 ± 8 |
| 4.15 | 0.21 | 0.96 | 0.0087 | 34 | ||||
| 4.73 | 0.16 | 0.92 | 0.0066 | 25 | ||||
| 6.50 | 0.13 | 0.97 | 0.0055 | 45 | ||||
| Bubble King Mini 160 needlewheel | 2.00 | 0.77 | 0.55 ± 0.1 | 0.014 | 0.011 ± 0.002 | 32 | 37 ± 6 | |
| 2.00 | 0.42 | 0.0084 | 30 | |||||
| 2.00 | 0.51 | 0.010 | 45 | |||||
| 2.00 | 0.50 | 0.0098 | 42 | |||||
| Royal Exclusiv 170 Cone needlewheel | 4.06 | 0.64 | 0.92 | 0.50 ± 0.10 | 0.017 | 0.014 ± 0.002 | 12 | 24 ± 12 |
| 4.06 | 0.43 | 0.97 | 0.012 | 39 | ||||
| 4.06 | 0.43 | 0.98 | 0.012 | 23 |
The analysis of Table 1’s data begins with a caveat; for some skimmers, the error bars (= “spread” of the measurements) in k are rather large, about 50% of the average value (cf. the EuroReef CS80 and the Precision Marine AP624). Therefore, it would not be appropriate to “over interpret” the significance of the differences in k values for the different skimmers. However, it is possible to use statistical techniques to arrive at an unbiased answer to the question, “Is skimmer A’s rate constant significantly different than skimmer B’s rate constant?”, where “significantly different” is defined as the chance that purely random sampling would result in the averages of two skimmer’s k values being as far apart as they are observed to be by experiment. This statistical technique is called an unpaired t-test, and its conclusions are really robust only for data sets containing far more entries than we have in Table 1. In actuality, there is no statistical test designed for data sets having as few as 3-5 entries, and so we will have to bear this caveat in mind when interpreting the t-test data. T-test statistical analysis of the rate constant’s k for the seven skimmers examined in this study suggest that:
- the k value for the Reef Octopus 150 skimmer is different than (smaller than) all of the other skimmers, and
- the rate constant k for the Precision Marine ES100 skimmer is different than (bigger than) the Bubble King and Royal Exclusive entries.
On the other hand, there are no statistically significant differences between the rate constants k for the EuroReef CS80, the Precision Marine ES100, the Precision Marine AP624 and the ETSS Evolution 500 skimmers. The rate constants k for the Bubble King and the Royal Exclusiv Cone are indistinguishable. Nevertheless, even the statistically significant differences in rate constants for TOC removal are not large, only spanning an approximately 10x range from the smallest to the largest. Since the rate constant k is an intrinsic measure of the skimmer’s ability to remove TOC, and it takes into account all of the physical factors that contribute to that removal (i.e., skimmer geometry, bubble size, bubble flow rate, foam coalescence characteristics, water characteristics, etc., etc.), there does not appear to be any compelling reason to favor one type of skimmer design/bubble generation mechanism over any other amongst the seven skimmers examined (Reef Octopus 150 excepted). That is, the inclusion or omission of a bubble plate does not seem to have any decisive effect on the rate constant for TOC removal, nor does a change in skimmer geometry from cylindrical to cone-shaped. Likewise, all methods of bubble generation examined appear adequate.
One question that impacts on the mathematical model derivation, especially the simplification discussed with Eq. (25), involves the relationship between the flow rate Q and the intrinsic rate constant k. There is no provision in the math that links these two quantities; however, if k does depend upon Q, then the simplification of Eq. (25) will not hold. This point was examined experimentally with the Reef Octopus 150 skimmer, as this skimmer has a recirculating pump for bubble introduction and hence the water flow rate Q should not influence the rate of bubble generation. Flow rates from 2.69 gal/min to 6.50 gal/min (= 162 gal/hr to 390 gal/hr) were examined. Within this flow regime, there was no significant variation in the derived rate constant k. So, at least for the Reef Octopus 150 skimmer, and by extension to all of the skimmers, we proceed with the analysis as if k is not dependent on water flow rate Q. Note that in the original January 2009 Advanced Aquarist publication, we attempted to examine the same point using the airstone skimmer (Precision Marine AP624). In those trials using BSA removal as the experimental parameter, we did observe a non-linear response between Q and k; Q = 156 gal/hr, k = 3.1 min-1; Q = 318 gal/hr, k = 7.6 min-1; Q = 540 gal/hr, k = 2.5 min-1. The basis for the discrepancy between the BSA/airstone skimmer results and the TOC/Reef Octopus results is not clear.
The overall rate of TOC removal, as modeled by the exponential term of Eq. (22), is a function of the rate constant k, the skimmer mixing volume Vs, and possibly the flow rate Q (see Eq. (25) and the accompanying discussion). Therefore it is perhaps a more relevant metric for answering overall questions about skimmer performance, since it takes into account the distinct operational parameters (flow, size) of each skimmer. For this metric, large error bars on the order of 10-40% of the average value once again suggest caution in (over) interpreting the data. There are t-test-based statistically significant differences in the values for this rate measurement amongst many the skimmers. Once again, the Reef Octopus 150 displays a rate that is significantly less than all of the other skimmers tested. The Bubble King and Royal Exclusiv skimmers do not display statistically significant differences in their rates of TOC removal, but both of these skimmers do operate at an appreciably slower rate of TOC removal than the Precision Marine ES100, the Precision Marine AP624, and the ETSS Evolution 500.
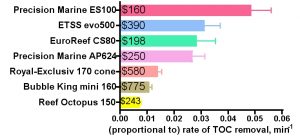
The skimmers all have different mixing volumes Vs, ranging from a maximum of 1.3 gallons for the Reef Octopus 150 down to a minimum of 0.69 gallons for the Bubble King and 0.62 gallons for the EuroReef. These differences in skimmer sizes become influential in determining the overall rate of TOC removal, whereas the flow rate Q has much less significance (see the discussion along with Eq. (25)). For example, the smallish Bubble King mini 160 skimmer has a relatively small overall rate of TOC removal even though its intrinsic rate constant k is in the middle range; that is, its smaller size really limits its ability to remove TOC rapidly. The similarly sized EuroReef CS80 has a much larger rate of TOC removal since its intrinsic rate constant k is 4x the Bubble King’s k value. Conversely, the large volume of the Reef Octopus 150 does not overcome an intrinsic rate constant k at the lower edge of the calculated values and so it exhibits the smallest rate of TOC removal amongst all of the skimmers tested. Of course, all of these skimmers arrive with different price tags, and so a relevant question might focus on the price/performance trade-off. These data are illustrated in Fig. 7. The prices listed are the standard retail price that was paid at the time that these skimmers were purchased. It should not escape notice that the least expensive skimmer (the Precision Marine ES100) offers the greatest rate of TOC removal.
In a practical sense, it is important to resist over interpreting these rate-of-TOC removal data. Most aquarists run their skimmer 24/7, and under that husbandry regime, the major impact of differing rates of TOC removal will be on how often the skimmer cup needs to be cleaned. If the skimmer removes TOC with a faster rate, then the cup will be filled faster and hence have to be cleaned sooner.
One of the more surprising and important observations to emerge from the earlier skimmer studies was that the four original skimmers tested removed only 20 – 30% of the measurable TOC in the reef tank water examined; the remaining 70 – 80% of the TOC was not removed by skimming. Extension of these measurements to the three new skimmers tested in this study did not add much to the argument. The Reef Octopus’ removal amount fell within this range, whereas the Bubble King and Royal Exclusiv skimmers appeared to remove incrementally more of the extant TOC, perhaps up to the mid-30% range. An explanation for this observation was offered in the January 2009 Advanced Aquarist article; in summary, skimmers can only remove what bubbles trap, and bubbles only trap molecules and/or particles (i.e., bacteria, diatoms, etc.) with some compelling thermodynamic reason to adhere to the bubble’s surface. On the molecular level, this surface association is typically driven by the molecule/particle having a hydrophobic (= water hating) patch that can be buried in the bubble surface/interior. This arrangement avoids the energetically penalizing juxtaposition of hydrophobic surfaces with (hydrophilic) water, and so overall the system energy is lowered (a favorable occurrence). Some of the molecules/particles in aquarium water will meet this hydrophobic region criterion, and some will not. The ones that do not have a sufficiently large hydrophobic patch will not interact with bubbles, and hence will not be removed by skimming. From, the results of the experiments described here, it appears that only 20 – 35 % of the measurable TOC meets this hydrophobicity criterion (= [TOCl] defined earlier) whereas the remaining 65 – 80 % does not (= [TOCr] defined earlier). In essence, bubbles are a rather poor media for removal of organic nutrients from aquarium water compared to, for example, GAC. However, they do have the distinct benefit of being cheap.
Conclusions
Many factors contribute to the “value” of a skimmer to an aquarist, including quality of construction, size, footprint, noise level, ease of cleaning, energy efficiency of the pump, and of course, the ability to remove organic waste from aquarium water. Our data show that there are not compelling or remarkably large differences in measurable skimmer TOC removal metrics among the seven skimmers tested, although the Reef Octopus 150 consistently underperformed compared to the other skimmers. However, in the larger picture, it is equally apparent that if an aquarist runs a skimmer continuously (24/7), then any of the skimmers tested would perform adequately in terms of rate of TOC removal; the only practical differences might involve the frequency of skimmer cup cleaning. A perhaps more interesting observation to emerge from these skimmer studies involves not the rate of TOC removal, but rather the amount of TOC removed. None of the skimmers tested removed more than 35% of the extant TOC, leading to the conclusion that bubbles are really not a very effective medium for organic nutrient removal. If fact, the presence of refractory, or unskimmable, TOC, coupled with the likelihood that endogenous TOC consumers (bacteria, among others) also do not remove all of the TOC present (cf. Fig. 4), suggest that in an operational sense, TOC can be categorized as follows:
- TOC that a skimmer removes
- TOC that a skimmer does not remove
- TOC that is consumed by microbes
- TOC that is not consumed by microbes
- TOC that is (indirectly or directly) harmful to tank livestock
- TOC that is not harmful to tank livestock
The last two categories must be included as a result of recent work of Forest Rohwer (See the January 2009 Advanced Aquarist article for a discussion), and they really highlight why an aquarist might be concerned with rising tank TOC levels. Of course, there will be much overlap between these categories. Ultimately, the crucial question for sustaining aquarium livestock health over the long term is, “How much of the harmful TOC (#5) is removed by either biological consumption or by skimming?” That question remains unanswered at present.
The results to date on protein skimming as a means of aquarium water remediation form a consistent picture that is at odds with some of the cherished dogma in the marine husbandry area. According to the data presented in this and the earlier paper (Advanced Aquarist, January 2009), protein skimmers appear to have a much larger variation in their prices than they do in their ability to remove TOC from aquarium water. Recent design innovations like bubble plates, conical sides, or pinwheel impellers do not seem to impact significantly on either rate of TOC removal or amount of TOC removed, at least for the skimmers tested. Thus, skimmer manufacturer claims about enhanced organic removal capabilities should be met with skepticism in the absence of compelling and quantitative TOC removal data.
Acknowledgments
We thank the Eberly College of Science at the Pennsylvania State University and E. I DuPont de Nemours and Co. for financial support, Dr. Bruce Logan and Mr. David Jones of the Pennsylvania State University Department of Civil and Environmental Engineering for use of the Shimadzu 5000 TOC Analyzer, Dr. James Vrentas of the Pennsylvania State University Department of Chemical Engineering for assistance in developing the mathematical model described in this article, and Dr. Sanjay Joshi for the use of his reef tank and for many helpful discussions.
References
- Allers, E.; Niesner, C.; Wild, C.; Pernthaler, J. 2008. “Microbes Enriched in Seawater after Addition of Coral Mucus.” Appl. Environ. Microbiol., 74, 3274-3278.
- Covert, J. S.; Moran, M. A. 2001. “Molecular Characterization of Estuarine Bacterial Communities that Use High- and Low-Molecular Weight Fractions of Dissolved Organic Carbon.” Aquat. Microb. Ecol., 25, 127-139.
- de Goeij, J. M.; van Duyl, F. C. 2007. “Coral Cavities are Sinks of Dissolved Organic Carbon.” Limnol. Oceanogr., 56, 2608-2617.
- Felder, R. M.; Rousseau, R. W. 2005. Elementary Principles of Chemical Processes, 3rd Ed., John Wiley and Sons, New York.
- Feldman, K. S.; Maers, K. M.; Vernese, L. F.; Huber, E. A.; Test, M. R. 2009. “The Development of a Method for the Quantitative Evaluation of Protein Skimmer Performance.” Advanced Aquarist http://www.advancedaquarist.com/2009/1/aafeature2/
- Kirchman, D. L. 1990. “Limitation of Bacterial Growth by Dissolved Organic Matter in the Subartic Pacific.” Mar. Ecol. Prog. Ser., 62, 47-54.
- Mopper, K.; Stubbins, A.; Ritchie, J. D.; Bialk, H. M.; Hatcher, P. G. “Advanced Instrumental Approaches for Characterization of Marine Dissolved Organic Matter: Extraction Techniques, Mass Spectrometry, and Nuclear Magnetic Resonance Spectroscopy.” Chem. Rev., 107, 419-442.
- Sharon, G.; Rosenberg, E. 2008. “Bacterial Growth on Coral Mucus.” Curr. Microbiol., 56, 481-488.
- Wild, C.; Rasheed, M.; Werner, U.; Franke, U.; Johnstone, R.; Huettel, M. 2004. “Degradation and Mineralization of Coral Mucus in Reef Environments.” Mar. Ecol. Prog. Ser., 267, 159-171.
- Zweifel, U. L.; Norrman, B.; Hagström, A. 1993. “Consumption of Dissolved Organic Carbon by Marine Bacteria and Demand for Inorganic Nutrients.” Mar. Ecol. Prog. Ser., 101, 23-32.




0 Comments